Polynomials
Roots and Logarithms
-
-
-
Trigonometry and Polar Coordinates
-
Trigonometric functions:
-
Cartesian coordinates:
-
Polar coordinates:
-
Spherical coordinates, cylindrical coordinates, etc.
Cartesian Coordinates
-
Descartes -> des Cartes -> Cartes -> Cartesian
-
In all coordinate systems there are origin and axis (plural: axes)
-
In Cartesian coordinate systems there are
quadrants (
octants(
hyperoctants(
Complex Numbers: Rectangular Form
-
-
-
-
Complex Numbers: Polar Form
Complex Numbers: Special Sets
-
(
-
(open) unit disk / disc:
-
unit circle:
Game
-
Shuffle the 52-cards deck and place 10 cards in a row on the table
-
Two players take turns to pick cards. In each turn the player chooses one end of the row and pick a card from that end
-
The player with more points after 10 turns wins. Play and find a good strategy for the first player
Round 1










Round 2










Round 3










Round 4










Functions and Maps
-
-
Roots and Support Sets
-
If
Alternatively:
In certain context: -
The closure of the set
Injectivity and Surjectivity
-
Injectivity: If
-
Surjectivity: If every
-
Bijectivtity: If
Onto and Into
-
-
Equations and Expressions
-
Equation: a+b=c
Inequality: a+b>c
Expression: a+b -
-
Laws of Operations
-
A binary operation
a -
A binary operation
a+(b+c)=(a+b)+c -
Given binary operations
Parentheses, Brackets and Braces
-
-
-
Sufficiency and Necessity
-
-
they are equivalent
Definition(Dyck Paths). A Dyck path of length
Example and Nonexample
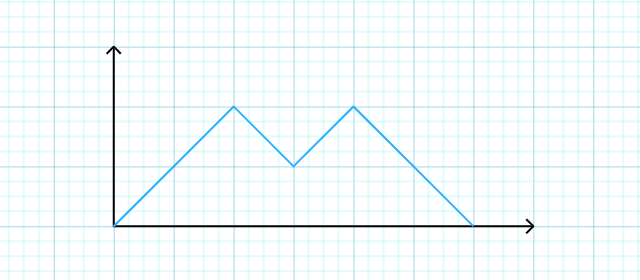
Definition(Catalan Numbers). The Catalan number
Theorem. The total number of Dyck paths of length
Conventions
-
A definition should be both precise and minimal
-
If a defintion is not straightforward, or counterintuitive or concerns subtle delicate cases, then it would be a good practice to include examples and/or nonexamples
-
It is often good to explain the motivation
Types of Example
-
Example
-
Nonexample
-
Counterexample
Tasks
Give a definition for continuous functions on
provide some examples and nonexamples
Summary
-
Elementary functions
-
Complex numbers
-
Coordinates and expressions
-
Definitions, examples, nonexamples