Sets

• a set is a collection of objects
  
  
• an element of a set is a member of it
  
  
• the empty set:
  
  
• example:

Notations

• membership:
  
  
• subset:
  
  
• proper subset:
  
  
• power set: the collection of all subsets of a given set

Finite and Infinite

• finite set:
  
  

• infinite set:
  
  

• the order of a finite set is the amount of elements in it, denoted by
  
  

• an infinite set can be either countable or uncountable

Notations

• union:
  
  
• intersection:
  
  
• complement:
  
  
• differrence:
  
  
• (direct) product:

Exercises

• the union of rational numbers and irrational numbers is ?
  
  

• the intersection of rational numbers and irrational numbers is ?
  
  

• give an example of infinite such that
  , ,
  
  

• the order of the power set of is ?

Maps

• given sets
  
  

• a map is a rule (or a collection of rules) so that for any , there is a unique and deterministic that corresponds to it according to the rule/rules
  
  

• is called the image of , while is called the pre-image of , we will denote such correspondence by
  
  

Notations

Bijectivity

• surjection：every element in has a pre-image in ( is onto )
  
  

• injection： implies
  
  

• bijection：a map that is both a surjection and an injection
  
  

• a map is said to be surjective/injective/bijective if it is a surjection/injection/bijection

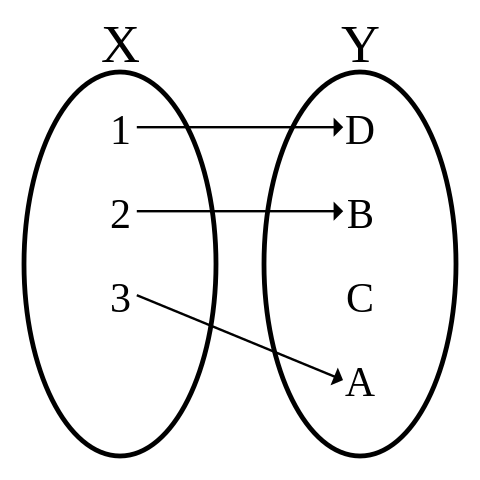
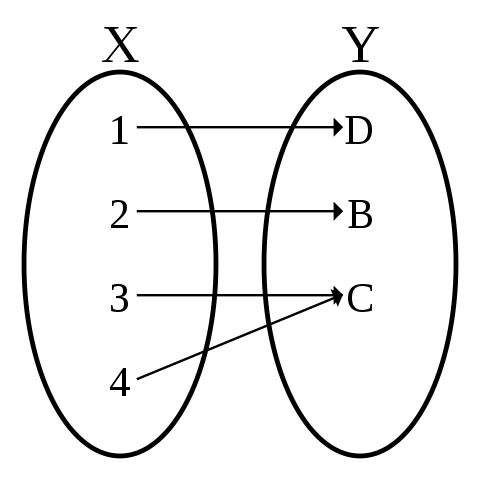
Exercises

• decide whether following maps are injective / surjective / bijective
  
  

• X: students in this class, Y: male, female, f: gender
  
  

• X: students in this class, Y: student numbers, f: the correspondence
  
  

• X: students in this class, Y: , f: age

Composition

• given , ，and
  
  

• the map ，is called the compostion of and ，and denoted by
  
  

• Attention: the ordering matters here, is not

Inverse

• if is injective, then reverting the correspondence gives the inverse map of
  
  

• example: with
  then with
  
  

• is the identity map

Domain and Range

• given
  
  

• domain of : the subset of on which is well defined
  
  

• range of : the set of all possible values of

Examples and Exercises

• with
  domain of :
  range of :
  
  

• find domains and ranges of
  with
  with

Graphs

• given a function on
  
  

• each pair corresponds to a point in the Cartesian coordinate system
  
  

• the set of all such points is the graph of the function

Monotonicity

• a function is monotonic if it is entirely non-increasing or non-decreasing
  
  

• monotonically increasing: implies
  monotonically decreasing: implies
  monotonically non-decreasing: implies
  monotonically non-increasing: implies
  
  

Symmetricity and Periodicity

• given a function on
  
  

• is even if , example:
  is odd if , example:
  
  

• is periodic if ，s.t. holds
  example:

Boundedness

• given a function on
  
  

• is upper bounded if ，s.t. holds
  is lower bounded if ，s.t. holds
  is bounded if it is both upper and lower bounded
  
  

• upper/lower bounded: there is a horizontal line above/below the graph of the functions

Exercises

• Decide whether and how the following functions are bounded:
  
  

• 
  
  

• Decide whether： is periodic

Summary

• Maps, Functions, and Graphs
  
  
• Injection, Surjection, Bijection, Composition, Inversion
  
  
• Monotonicity, Boundedness, Periodicity, Even/Oddness
  
  
• Elementary Functions