正方向
"外":逆时针方向
"内":顺时针方向

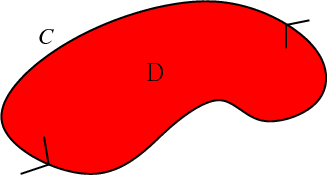

格林公式
设闭区域
简单情况的证明
-
设
-
也能写成
-
其中
简单情况的证明
例子
-
求
-
令
-
原式
-
若用上节方法直接计算:
练习
积分与路径无关
设
且
证明的主要步骤
-
先证:
-
设
-
若
证明的主要步骤
-
再证:
-
设
不妨设 -
则存在
-
从而
证明的主要步骤
-
再证:
-
若
-
因
证明的主要步骤
-
再证:
-
若
-
则
(类似于一元函数的微积分基本定理)
证明的主要步骤
-
-
在
-
上式
-
利用积分中值定理可得
以下几个命题等价
若
-
-
-
-
练习
对以下函数,计算
这一条件对上述等价命题和格林公式不可或缺
小结
- 格林公式及其物理意义
- 积分与路径无关的几个等价命题