如图:
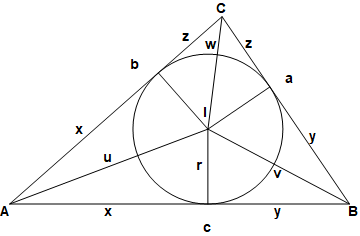
令
$$s=\frac{a+b+c}{2}=x+y+z$$
为三角形的半周长,则
$$x=s-a, \quad y=s-b, \quad z=s-c$$
内切圆半径
$$r^2=\frac{xyz}{x+y+z}=\frac{(s-a)(s-b)(s-c)}{s}$$
IA, IB, IC即$u,v,w$,满足
$$u^2=r^2+x^2, \quad v^2=r^2+y^2, \quad w^2=r^2+z^2$$
此处的难点是要验证$r$事实上是整数,接下来就可以生成所有勾股数组再取满足要求的作为$u,v,w,x,y,z,r$,或用
$$r^2=(u-x)(u+x)=(v-y)(v+y)=(w-z)(w+z),$$
来遍历$r^2$的约数以生成$u\pm x, v\pm y, w\pm z$,两者的计算量相仿。
要证明$r$是整数首先可以验证
$$r=\frac{suvw}{abc}.$$
因此$r$是有理数。
其次注意到
$$2r=\sqrt{4u^2-4x^2},$$
而等式左侧是有理数,等式右侧是整数的平方根,因此$2r$事实上是整数。
最后,若$r$不是整数,则$2r$只能是奇数,从而$4r^2$模$4$余$1$。另一方面,$u$是整数,因此$4u^2$模$4$余$0$,而$4x^2=(b+c-a)^2$模$4$或者余$0$或者余$1$,从而$4r^2=4u^2-4x^2$或者能被$4$整除,或者模$4$余$3$,矛盾。因此$r$必然是整数。
最终结果是$1400824879147$。
注:因用到math.isqrt函数,以下代码为Python 3,代码中还打印了进度信息。
import math
target=10**7
bound=target//3
primeFactorMax=[1]*(bound)
for i in range(2,bound):
if primeFactorMax[i]==1:
for j in range(i,bound,i):
primeFactorMax[j]=i
tick=bound//100
res=0
for i in range(1,bound):
d=[1]
n=i
while n>1:
r=len(d)
p=q=primeFactorMax[n]
while n%p==0:
for j in range(r):
d.append(q*d[j])
d.append(p*q*d[j])
n//=p
q*=p*p
d.sort()
sq=[(d[-1-j]-d[j])//2 for j in range(len(d)//2-1,-1,-1) if (d[-1-j]-d[j])%2==0]
sqSet=set(sq)
for j in range(len(sq)):
x=sq[j]
if x>bound//2:
break
for k in range(j,len(sq)):
p=sq[k]
if x+p>bound:
break
if x*p==i*i:
continue
q,r=divmod(i*i*(x+p),x*p-i*i)
if r or q < p or q not in sqSet or x+p+q>target//2:
continue
res+=2*(x+p+q)+math.isqrt(x*x+i*i)+math.isqrt(p*p+i*i)+math.isqrt(q*q+i*i)
if i%tick==0:
print(i//tick, "percent completed, current result:", res)
print(res)
|