椭圆内接三角

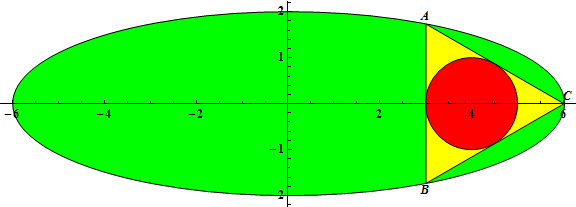
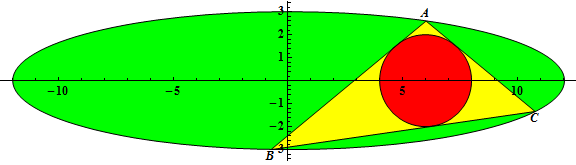
给定椭圆$x^2/a^2+y^2/b^2=1$，其中$0 < 2b < a$，且a和b均为整数。 三角形ABC内接于此椭圆，且其内接圆圆心是$(2b, 0)$，A点坐标是$(a/2, \sqrt3 b/2)$，令$r(a,b)$为此三角形内接圆的半径。 可以验证$r(3,1)=1/2, r(6,2)=1, r(12,3)=2$。再令 $$G(n)=\sum_{a=3}^n\sum_{b=1}^{\left\lfloor\frac{a-1}{2}\right\rfloor}r(a,b), $$ 则可以验证$G(10)\approx20.59722222, G(100)\approx19223.60980$（均保留10位有效数字）。 求$G(10^{11})$，并将结果用10位有效数字的科学计数法表示，用小写字母e来分割尾数和指数，例如$G(10)$按这一规则应写作$2.059722222e1$。

本题难度:

解答

可以验证 $$r(a,b)=b-\frac{b^2}{a-b}.$$ 令$c=a-b$，$m_a=\lfloor(a-1)/2\rfloor$则有 \begin{align*} G(n)&=\sum_{a=3}^n\sum_{b=1}^{m_a}b-\frac{b^2}{a-b} \\, &=\left(\sum_{a=3}^n\frac{m_a(1+m_a)}{2}\right)+\sum_{c=a-m_a}^{a-1}\sum_{a=3}^n\frac{(a-c)^2}{c} \\ &=\frac{1}{2}\left(\sum_{a=3}^n m_a^2+m_a\right)+\sum_{c=a-m_a}^{a-1}\frac{1}{c}(\frac{n(n+1)(2n+1)}{6}-5)-n(n+1)+6+(n-2)c \\ \end{align*} 代入$n=10^{11}$后以上各项和式用Wolfram Alpha等工具即可计算，最终结果是$1.895093981e31$。 本题无需编程。