刚性图

图是由一系列点和连接点的边所组成的集合，由一条边所连接的两点互为邻接点。

只需给每个点赋予坐标，就可以把图嵌入到欧氏空间中。

若存在一种将图中一个或多个点连续改变位置，使得任意一对邻接点的距离不变，但至少有两个非邻接的点的距离发生了变化的方式，就称该图为非刚性图，否则称其为刚性图。

直观而言，若把图中的点想像成可自由旋转的铰链，把边想像成成不可弯折且无弹性的木棒，则刚性图的任意局部都不能独立于其它部分而移动。

平面上的方格图是非刚性图，以下是两种移动方式：

但若在其中的一些方格内添加对角线，则其会成为刚性图，对$2\times3$的方格图而言，共有如下19种添加对角线的方式：

本题中的方格只有有对角线和无对角线两种状态，其方向和数量不论，所有方格的状态相同即认为是同一种添加方式。

记$R(m,n)$为通过添加对角线将$m\times n$方格图变为刚性图的方法总数，例如$R(2,3)=19$，可以验证$R(5,5)=23679901$。

再定义$S(N)=\sum_{1\le i,j\le N}R(i,j)$，可以验证$S(5)=25021721$。

求$S(100)$模1000000033的余数。

本题难度:

解答

本题看似复杂，但解法很巧妙，以下说明和图均来自官方论坛：

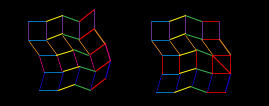
由于邻接点的距离保持不变，从而在移动的过程中，每个小方格的对边都始终保持平行，这一性质在行与列之间传递，因此位于同一行和位于同一列的对边始终保持平行，如下图（相互平行的边用同色标识）：

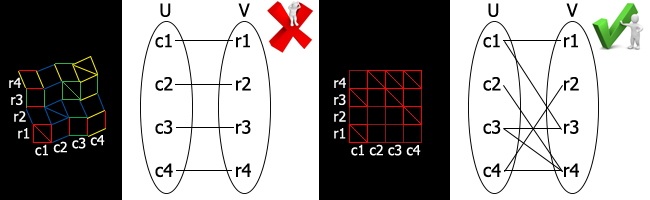
在小方格中添加对角线可以迫使其邻边在移动后保持相互垂直的状态，要使图具有刚性，需要所有的行和列都保持相互垂直（正如初始状态）。

在第$(x,y)$格中添加对角线，可使x行和y列保持垂直，为能使所有的行和列都相互垂直，考虑由行标和列标组成的集合U和V，将其理解为一个二分图，每添加一条对角线就是在此二分图中添加一条两端分别在U和V中的边，所有的行和列都相互垂直即此二分图连通，从而本题转化为求连通二分图的总数。

显然U和V之间的二分图共有$2^{mn}$个，其中不连通的二分图可以视作将原图分割为一系列连通子图，从而有 $$R(m,n)=2^{mn}-\sum_{\{x,y: 0\le x\le m, 1\le y\le n, x+y < m+n,\}}\binom{m}{x}\binom{n-1}{y-1}R(x,y)2^{(m-x)(n-y)}.$$ 递推计算即得结果$863253606$。

N=100
MOD=10**9+33

comb=[[1]+[0]*N for i in range(N+1)]

for i in range(1, N+1):
    for j in range(1,N+1):
        comb[i][j]=(comb[i-1][j-1]+comb[i-1][j])%MOD

q=[1]
for i in range(N*N):
    q.append((2*q[-1])%MOD)

R=[[0]*(N+1) for i in range(N+1)]
for i in range(N+1):
    R[i][1]=R[1][i]=1

for m in range(1,N+1):
    for n in range(1,N+1):
        t=q[m*n]
        for x in range(m+1):
            for y in range(1,n+1):
                if x+y < m+n:
                    t-=comb[m][x]*comb[n-1][y-1]*R[x][y]*q[(m-x)*(n-y)]
        R[m][n]=t%MOD

print sum(R[m][n] for m in range(1,N+1) for n in range(1,N+1))%MOD