用一个四元组表示每个格子中四个面的状态,其中0表示这一面没有出入,1和2分别表示出和入,则合法的出入状态共有12种,如下图:
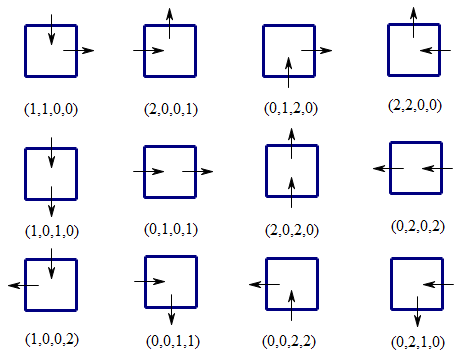
将这12种状态记作S,则两个相邻格子的状态,取决于其相对位置,只能是$S\times S$中的一些特定元素。
先搜索出所有的合法状态的组合。
然后枚举第一行的状态,之后每一行的状态都可以根据上一行以及该行本身递推产生,最后汇总得结果$112398351350823112$。
N=10
M=3**N
squares=[
[1, 1, 0, 0], [2, 0, 0, 1], [0, 1, 2, 0], [2, 2, 0, 0],
[1, 0, 1, 0], [0, 1, 0, 1], [2, 0, 2, 0], [0, 2, 0, 2],
[1, 0, 0, 2], [0, 0, 1, 1], [0, 0, 2, 2], [0, 2, 1, 0]
]
g=[[] for i in range(M)]
def dfs(t,c,u,v):
if t==N:
if c==0:
g[u].append(v)
return
for s in squares:
if s[3]==c:
dfs(t+1,s[1],u*3+s[0],v*3+s[2])
f=[[0]*M,[0]*M]
dfs(0,0,0,0)
f[0][0]=1
for i in range(N):
j=i%2
f[1-j]=[0]*M
for u in range(M):
for v in g[u]:
f[1-j][v]+=f[j][u]
print(f[N%2][0])
|