内接椭圆
|
给定平面上的三角形T,可以证明所有完全包含在T内部的椭圆中面积最大的椭圆是唯一的。
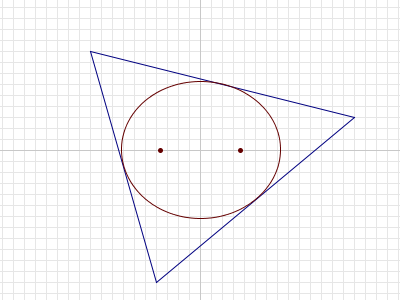
给定的n,考虑这样的三角形T:
(1)T的各顶点坐标均为绝对值不超过n的整数。
(2)T内面积最大的椭圆的焦点坐标是$(\pm\sqrt{13},0)$。
记$A(n)$为所有这样的三角形的面积之和。
例如当$n=8$时有两个这样的三角形。其顶点分别是$(-4,-3), (-4,3), (8,0)$和$(4,3), (4,-3), (-8,0)$,两者面积均为36。因此$A(8)=36+36=72$。
可以验证,$A(10)=252, A(100)=34632, A(1000)=3529008$。
求$A(10^9)$。
|
本题难度:
|
解答
|
这一类椭圆称为Steiner Inellipse,根据该页面的信息,它的面积可以由三角形的面积得到。
椭圆的焦点则由Marden给出,即若三角形的三个顶点在复平面上分别对应$z_1,z_2,z_3$,则此椭圆的两个焦点是恰是三次多项式$(z-z_1)(z-z_2)(z-z_3)$的两个根。
这些三角形顶点的分布带有明显的特征,见下图(图片来自官方论坛)
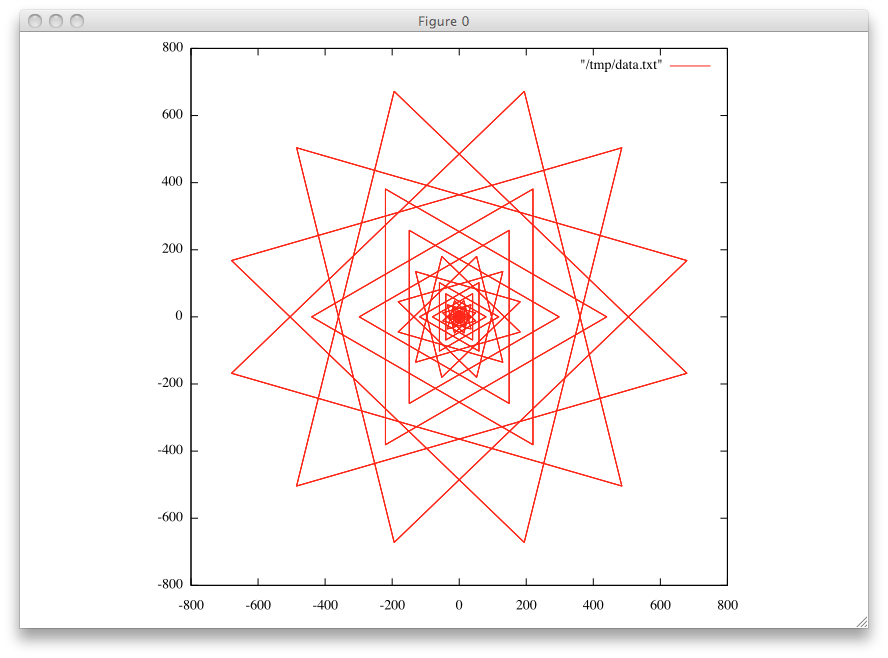
亦即所有的解系可以分解为由若干个基本解生成的轨道,具体计算比较繁琐,以下代码改编自官方论坛,最终结果是$3776957309612153700$。
R=10**9
A=0
for i,(p,q) in enumerate(((4,3),(5,6),(2,3))):
while 2*p<=R and (i<2 or 4*q<=R):
A+=6*p*q if i<2 else 156*p*q
p,q=2*p+q,3*p+2*q
print A
|
| |