贝塞尔曲线

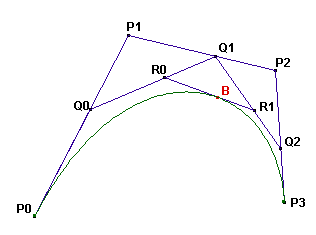
四个点$P_0, P_1, P_2, P_3$可以确定一条立方贝塞尔曲线，方式如下： 在线段$P_0P_1, P_1P_2, P_2P_3$上分别取点$Q_0, Q_1, Q_2$，使之满足 $$\frac{P_0Q_0}{P_0P_1}=\frac{P_1Q_1}{P_1P_2}=\frac{P_2Q_2}{P_2P_3}=t\in [0,1],$$ 在线段$Q_0Q_1$和$Q_1Q_2$上，再分别取点$R_0$和$R_1$，使之满足 $$\frac{Q_0R_0}{Q_0Q_1}=\frac{Q_1R_1}{Q_1Q_2}=t,$$ 最后在线段$R_0R_1$上取点B，使得 $$\frac{R_0B}{R_0R_1}=t,$$， 那么由$P_0, P_1, P_2, P_3$所即t取遍0到1之间的值时B点的轨迹。 由此构造过程可知该曲线在$P_0$处与线段$P_0P_1$相切，在$P_3$处与$P_2P_3$相切。 由$P_0=(1,0)$、$P_1=(1,v)$、$P_2=(v,1)$和$P_3=(0,1)$所确定的立方贝塞尔曲线可以用来近似表示四分之一的圆周。 适当选取$v>0$，由线段$OP_0$、$OP_3$（O是原点）和该曲线所包围的面积可以等于$\pi/4$（四分之一圆的面积）。 此时该曲线的长度与四分之一圆弧的长度相差百分之多少？ 亦即，若此时该曲线的长度为L，试求 $$100\times\frac{L-\frac{\pi}{2}}{\frac{\pi}{2}}$$ 结果保留小数点后10位数字。

本题难度:

解答

由构造的方式容易列出该曲线的参数方程： \begin{align*} x(t)&=(1-t)^3+3t(1-t)^2+3t^2(1-t)v,\\ y(t)&=3t(1-t)^2v+3t^2(1-t)+t^3, \end{align*} 用格林公式计算其面积： $$\frac{\pi}{4}=\frac{1}{2}\int_{\Omega}xdy-ydx,$$ 其中$\Omega$是$OP_0$、$OP_3$和该曲线所围成的区域，由此可以解得 $$\frac{\pi}{4}=\frac{1}{2}(1+\frac{6v}{5}-\frac{3v^2}{10}),$$ 即 $$v=2\pm\sqrt{\dfrac{1}{3}(22-5\pi)},$$ 根据题意应选择能使曲线近似于四分之一的圆周的v，用例如Desmos等应用作图可知应取$v=2-\sqrt{\dfrac{1}{3}(22-5\pi)}$（取+号时所得的曲线为绶带状）。 最后计算积分 \begin{align*} L&=\int_0^1\sqrt{\left(x'(t)\right)^2+\left(y'(t)\right)^2} dt \\ &=\int_0^1\sqrt{18(3v-2)^2t^4-36(3v-2)^2t^3+18(13v^2-14v+4)t^2-36(2v^2-v)t+9v^2}dt \end{align*} 用Wolfram等应用计算出其近似值后再与$\pi/2$比较即可得结果$0.0000372091$。 本题无需编程。 注：贝塞尔曲线一般在《数值分析》类课程中涉及，但本解法中的微积分计算是我国《高等数学》课程中的标准内容。