放豆子
|
在柏拉图的天堂里,有无穷多只排成一列的碗。
每个碗中或者放有有限颗豆子,或者没有豆子。
有一个小孩在玩游戏,该游戏只允许一种操作:从任意一个碗中取出两颗豆子,然后在其相邻的两个碗中各放一颗。
当每个碗中都或者只有一颗豆子或者没有豆子时游戏结束。
例如,考虑两个相邻的碗中分别装有2颗和3颗豆子,而其它碗中都没有豆子的情况,经过八次操作之后游戏结束。
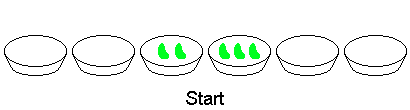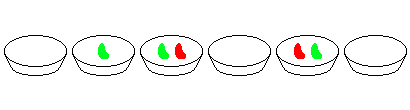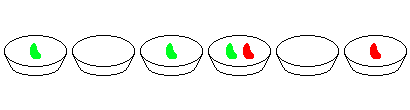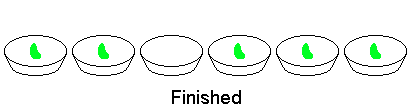
给定初值为$t_0=123456$,其余各项为
$$t_n=\begin{cases}\frac{t_{n-1}}{2} & t_{n-1}\text{为偶数,} \\ \frac{t_{n-1}-1}{2}\oplus926252 & t_{n-1}\text{为奇数,}\end{cases}$$
的序列,其中$\oplus$表示按二进制位异或。再令
$$b_n=(t_n \bmod 2^{11})+1,$$
则$b_1=289$,$b_2=145$。若相邻的两个碗中分别装有$b_1$和$b_2$颗豆子,其它碗中都没有豆子,则从这一状态开始到游戏结束共需要3419100次操作。
现考虑相邻的1500个碗中分别装有$b_1, \ldots, b_{1500}$颗豆子,其它碗中都没有豆子的情况,求到游戏结束所需要的操作次数。
|
本题难度:
|
解答
|
本题的解法十分巧妙。设操作总数为M,最终第j个碗里有$c_j$个豆子,其中$j\in\mathbb Z$,则可以注意到注意到如下四点:
(1)$\sum_{i\in\mathbb Z}b_i=\sum_{j\in\mathbb Z}c_j$,这是因为豆子的总数不变。
(2)$\sum_{i\in\mathbb Z}i\cdot b_i=\sum_{j\in\mathbb Z}i\cdot c_j$,这是因为整个系统的质心不变。
(3)2M+$\sum_{i\in\mathbb Z}i^2\cdot b_i=\sum_{j\in\mathbb Z}i^2\cdot c_j$,这是因为每次操作后整个系统的转动惯量增加了2。
(4)最终状态必定是一列连续的1中插入一个0的情形,这是因为用到的碗的数量恰比豆子的总数多一个。
先根据前两个等式找出最终状态中空碗的位置,再用第三个等式即可的结果$150320021261690835$。
注:质心和转动惯量的计算是我国理工科《高等数学》的课程内容之一。
注:以下为Python 3代码,以强调此处的除法均为整除。
m=n=m2=0
t=123456
for i in range(1, 1501):
t=(t//2)^((t & 1)*926252)
b=(t%2048)+1
n+=b
m+=b*i
m2+=b*i*i
d=(m//n)-(n//2)
z=(n+1)*(2*d+n)//2-m
print((((d+n)*(d+n+1)*(2*d+2*n+1)-d*(d-1)*(2*d-1))//6-z*z-m2)//2)
|
| |