自反位置

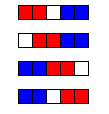
考虑以下组合博弈游戏： 游戏开始时，有一张划成n个白格的纸条，两名玩家轮流进行操作。 每轮中当前玩家需要选择两个相邻的白格，并将它们涂成黑色。 无法执行此操作的玩家输掉游戏。 若$n=1$，不存在合法操作，先手输。 若$n=2$，第一轮只有一种合法操作，后手输。 若$n=3$，第一轮有两种合法操作，仍是后手输掉。 若$n=4$，第一轮有三种合法操作，不过先手玩家只需将中间两个白格涂成黑色即可获胜。 若$n=5$，则第一轮有四种合法操作（如下图红色所示）；但无论先手玩家如何操作，后手玩家（蓝色所示）都将获胜。 因此，对于$\le n\le 5$，共有3种n值使得先手玩家必胜。类似地，对于$1\le n\le 50$，共有40种n值使得先手玩家必胜。 对于$1\le n\le 10^6$，共有多少种n值使得先手玩家必胜？

本题难度:

解答

本游戏实际上称为Dawson's Chess，OEIS A002187中给出了该游戏的胜负值（0表示先手负）。 除了n=0,14,16,17,31,34,51这几个位置以外，其他位置的n处胜负值都是以34为周期的序列，因此查表后手动求和即得结果$852938$。 本题无需编程。