本题非常麻烦,本人花费了大约三周左右的时间才找出答案。
本题中的地形连续变化,常规的思维是将其离散化再使用最短路径算法,但地图的范围是$1600\times 1600$,即使只用0.1的mesh size数据量也将十分庞大,且未必能达到要求的精度。因此首先需要找出最小高度$f_{min}$,再将其转化为平面问题。
先取1/3的间隔,从而将地图范围视作$4800\times 4800$的网格,计算出网格上所有点的高度并排序,随后二分查找可以从起点到达终点的最低高度。
对于每个给定的高度值f,将地图范围视作一张图,高度不超过f的点可以到达,超过f的点不可到达,每个点可以访问其相邻八个点中可以到达的点。
使用Dijkstra算法计算从 $(200,200)$到$(1400,1400)$之间是否存在通路,以下是计算最短高度的代码:
import math,heapq
height=lambda x,y:(5000-0.005*(x*x+y*y+x*y)+12.5*(x+y))*math.exp(-abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))
infty=999999999999
scale=3
mesh=1600*scale
sides=1/scale
diagonal=math.sqrt(2)/scale
ups=sorted([*{height(x,y) for x in range(mesh+1) for y in range(mesh+1)}])
a,b=0,len(ups)-1
while a < b-1:
c=(a+b)//2
z=ups[c]
reachable=False
d={(200*scale,200*scale):0}
q=[(0,200*scale,200*scale)]
visited=set()
while q and not reachable:
m,x,y=heapq.heappop(q)
k=x*mesh+y
if k not in visited:
visited.add(k)
if x==y==1400*scale:
reachable=True
break
for u,v in [(x-1,y-1),(x-1,y),(x-1,y+1),(x,y-1),(x,y+1),(x+1,y-1),(x+1,y),(x+1,y+1)]:
if 0 <= u <= mesh and 0 <= v <= mesh and height(u/scale,v/scale) <= z:
r=sides if u==x or v==y else diagonal
if d.get((u,v),infty)>d[(x,y)]+r:
d[(u,v)]=d[(x,y)]+r
heapq.heappush(q,(d[(u,v)],u,v))
if reachable:
b=c
else:
a=c
print("min height:",ups[b])
如此可得最小高度约为10396.462。这段代码耗时很长,且难以估计进度,需要耐心等待其运行。如取1/2的间隔,则精度只能达到小数点后两位。
接下来作图观察一下地形,以下是用matplotlib库作地形图的代码及生成的图片:
import math
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from matplotlib.ticker import LinearLocator
height=lambda x,y:(5000-0.005*(x*x+y*y+x*y)+12.5*(x+y))*math.exp(-abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))
step=0.5
fig=plt.figure()
ax=fig.add_subplot(projection='3d')
X=np.arange(0,1600,step)
Y=np.arange(0,1600,step)
Z=np.array([[height(x,y) for y in Y] for x in X])
X,Y=np.meshgrid(X,Y)
surf = ax.plot_surface(X,Y,Z,cmap=cm.coolwarm,linewidth=0,antialiased=False)
ax.set_zlim(0,20000)
ax.zaxis.set_major_locator(LinearLocator(20))
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.show()
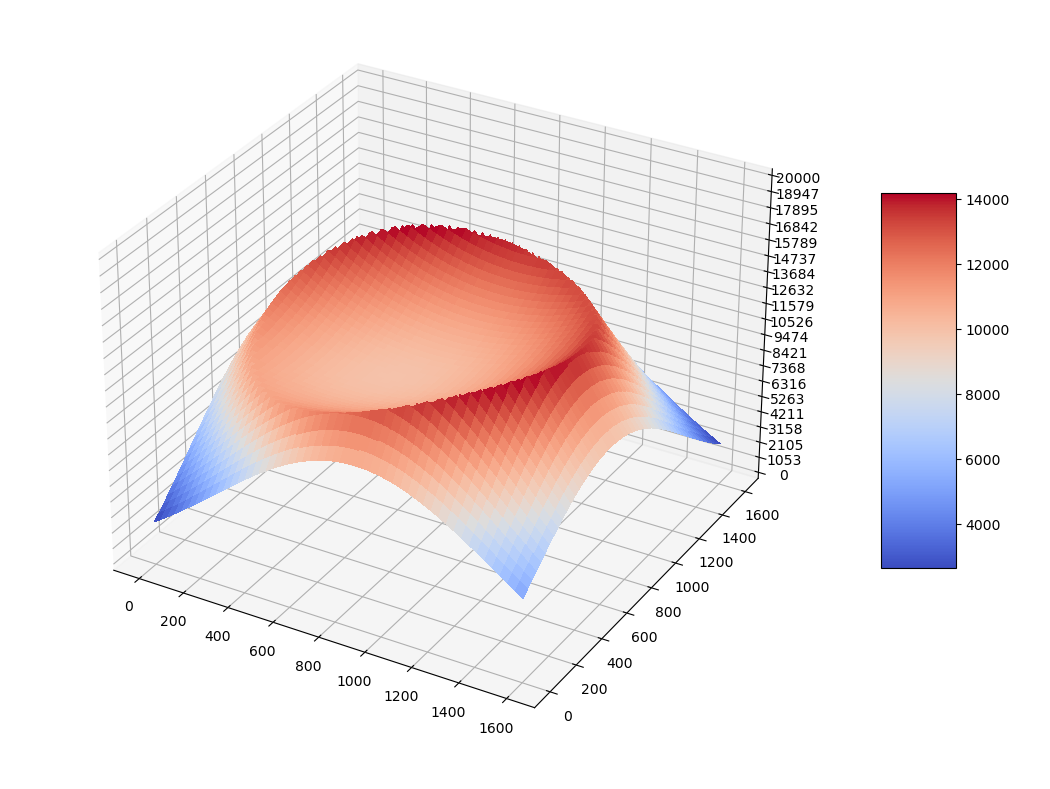
可以看出地形呈火山状,因数据范围很大,图片不太精细,但事实上主要的起伏都在火山口处。
从图中容易想到最短路径的策略应当不外乎先直线前进一段距离,直到遇到障碍,然后沿着等高线所在的圆弧运动一段距离,直到与终点之间无障碍,最后直线前进到终点。
这一走向大致是正确的,但并非最优路径,这是因为显然在沿着等高线的圆弧运动需要移动的距离更多,所以应当尽可能减少这部分移动的长度。
上述策略可以改进为:在等高线上取一点,该点出的切线恰能通过起点(或尽可能接近),从起点处直接沿着这条切线运动进入等高线(这一过程类似跑步或赛车时入弯的最短路径)。
具体实现时,先预设合理的步长,此处取0.0001。从起点$(200,200)$出发,不断沿着直线方向向终点$(1400,1400)$运动,直到无法前进,就达到了所需要进入的等高线。
接下来沿着等高线向终点移动充分远的距离(此处取1500),并计算每一点处与起点$(200,200)$练习的斜率,并与该点处的切线斜率比较,记录下差异最小的点,就是切入点。
此处涉及到的计算有
- 沿着等高线的运动:利用梯度垂直于等高线的切线这一性质,先计算出当前点的梯度,然后在两个正交的方向中取移动后离目的地更近的作为移动方向。
- 梯度计算:直接用公式计算,注意由于表示式中有绝对值,事实上可能存在一些不可微的点,不过此处似乎可以忽略这一情形。此外,由于表达式具有对称性,容易看出$f_y(x,y)=f_x(x,y)$。
- 切线斜率:由多元隐函数求导法则可知切线斜率是$-f_x/f_y$。
类似地,交换上文中的终点和起点就可以求得切出点。以下是上述计算的代码:
import math
height=lambda x,y:(5000-0.005*(x*x+y*y+x*y)+12.5*(x+y))*math.exp(-abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))
sub=lambda x,y: math.exp(-(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))*(-(0.000001*(2*x)-0.0015)) if 0.000001*(x*x+y*y)-0.0015*(x+y)+0.7>=0 else math.exp(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7)*(0.000001*(2*x)-0.0015)
partial=lambda x,y:(-0.005*(2*x+y)+12.5)*math.exp(-abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))+(5000-0.005*(x*x+y*y+x*y)+12.5*(x+y))*sub(x,y)
norm=lambda x,y:math.sqrt(x*x+y*y)
colinear=lambda x,y,a,b:abs(partial(x,y)*(x-a)+(y-b)*partial(y,x))
def findTangent(x1,y1,x2,y2,z,h,limit=1500):
x,y=x1,y1
r=norm(x-x2,y-y2)
dx,dy=(x2-x)/r,(y2-y)/r
while height(x+h*dx,y+h*dy) <= z:
x,y=x+h*dx,y+h*dy
r=norm(x-x2,y-y2)
dx,dy=(x2-x)/r,(y2-y)/r
print(f"Stopped at ({x,y,height(x,y)})")
j=0
mt=99999999
mx=my=-1
while j*h < limit:
dx,dy=partial(x,y),partial(y,x)
r=norm(dx,dy)
dx,dy=h*dx/r,h*dy/r
u1,v1=x-dy,y+dx
u2,v2=x+dy,y-dx
m1,m2=norm(x2-u1,y2-v1),norm(x2-u2,y2-v2)
if m1 < m2:
if 0 <= u1 <= 1600 and 0 <= v1 <= 1600:
x,y=u1,v1
else:
break
else:
if 0 <= u2 <= 1600 and 0 <= v2 <= 1600:
x,y=u2,v2
else:
break
t=colinear(x,y,x1,y1)
if t < mt:
mt,mx,my=t,x,y
j+=1
if j*h==limit:
print("completed")
else:
print(f"stucked at {x,y}")
return mx,my,norm(mx-x1,my-y1),mt
z=10396.462
x=y=200
a=b=1400
h=0.0001
u,v,d,t=findTangent(x,y,a,b,z,h)
print(f"Tangent in at{u,v,height(u,v)}, with distance {d}, tangents {t}")
u,v,d,t=findTangent(a,b,x,y,z,h)
print(f"Tangent out at{u,v,height(u,v)}, with distance {d}, tangents {t}")
根据运行的结果,切入点大约是$(624.651,48.253)$,切出点大约是$(873.039,1536.042)$,切入前/切除后各自需要移动的直线距离分别大约是450.948和544.238。
有高度函数的对称型可以看出$(1536.042, 873.039)$也可以是切出点,而从该点移动到$(624.651,48.253)$显然更近,因此以这一点作为切出点。
最后,计算等高线上这两点间的测地线距离,代码如下,最终结果是$2531.205$。
import math
height=lambda x,y:(5000-0.005*(x*x+y*y+x*y)+12.5*(x+y))*math.exp(-abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))
sub=lambda x,y: math.exp(-(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))*(-(0.000001*(2*x)-0.0015)) if 0.000001*(x*x+y*y)-0.0015*(x+y)+0.7>=0 else math.exp(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7)*(0.000001*(2*x)-0.0015)
partial=lambda x,y:(-0.005*(2*x+y)+12.5)*math.exp(-abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))+(5000-0.005*(x*x+y*y+x*y)+12.5*(x+y))*sub(x,y)
norm=lambda x,y:math.sqrt(x*x+y*y)
def getGeodesic(x,y,a,b,h,epsilon,limit):
j=0
d=99999999
while d>epsilon and j*h < limit:
dx,dy=partial(x,y),partial(y,x)
r=norm(dx,dy)
dx,dy=h*dx/r,h*dy/r
u1,v1=x-dy,y+dx
u2,v2=x+dy,y-dx
m1,m2=norm(a-u1,b-v1),norm(a-u2,b-v2)
if m1 < m2:
if 0 <= u1 <= 1600 and 0 <= v1 <= 1600:
x,y=u1,v1
else:
break
else:
if 0 <= u2 <= 1600 and 0 <= v2 <= 1600:
x,y=u2,v2
else:
break
d=norm(a-x,b-y)
j+=1
if d < epsilon:
print(f"Completed with {j} steps, total distance {450.948315086643+544.2381822641057+j*h}")
elif j*h==limit:
print("Not Found")
else:
print(f"Stucked at {x,y}")
return j*h,x,y
x,y,r1=624.6510689712037,48.253075473368014,450.94973054840307
b,a,r2=873.0389052039443,1536.0424611611559,544.2385016400826
h=0.0001
mx=my=mj=-1
limit=2500
epsilon=1
d1,x1,y1=getGeodesic(x,y,a,b,h,epsilon,limit)
d2,x2,y2=getGeodesic(a,b,x,y,h,epsilon,limit)
print(r1+r2+d1+d2+norm(x1-x2,y1-y2))
实际运行中可以发现在测地线在某一位置处十分靠近地图边界,此处的等高线方向不易处理,因此从上面的代码中从起点和终点分别出发计算测地线,最后在地图边界处直接将两者相连(距离为1左右)。
把上面的代码稍加修改可以绘制出路线图,绘图代码和所得的图片如下:
import math
import matplotlib.pyplot as plt
import numpy as np
from matplotlib import cm
from matplotlib.ticker import LinearLocator
height=lambda x,y:(5000-0.005*(x*x+y*y+x*y)+12.5*(x+y))*math.exp(-abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))
sub=lambda x,y: math.exp(-(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))*(-(0.000001*(2*x)-0.0015)) if 0.000001*(x*x+y*y)-0.0015*(x+y)+0.7>=0 else math.exp(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7)*(0.000001*(2*x)-0.0015)
partial=lambda x,y:(-0.005*(2*x+y)+12.5)*math.exp(-abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7))+(5000-0.005*(x*x+y*y+x*y)+12.5*(x+y))*sub(x,y)
norm=lambda x,y:math.sqrt(x*x+y*y)
def getGeodesicPath(x,y,a,b,h,epsilon,limit):
pathx=[x]
pathy=[y]
pathz=[height(x,y)]
j=0
d=99999999
while d>epsilon and j*h < limit:
dx,dy=partial(x,y),partial(y,x)
r=norm(dx,dy)
dx,dy=h*dx/r,h*dy/r
u1,v1=x-dy,y+dx
u2,v2=x+dy,y-dx
m1,m2=norm(a-u1,b-v1),norm(a-u2,b-v2)
if m1 < m2:
if 0 <= u1 <= 1600 and 0 <= v1 <= 1600:
x,y=u1,v1
else:
break
else:
if 0 <= u2 <= 1600 and 0 <= v2 <= 1600:
x,y=u2,v2
else:
break
d=norm(a-x,b-y)
j+=1
pathx.append(x)
pathy.append(y)
pathz.append(height(x,y))
if d < epsilon:
print(f"Completed with {j} steps, total distance {450.948315086643+544.2381822641057+j*h}")
elif j*h==limit:
print("Not Found")
else:
print(f"Stucked at {x,y}")
return pathx,pathy,pathz
x,y,r1=624.6510689712037,48.253075473368014,450.94973054840307
b,a,r2=873.0389052039443,1536.0424611611559,544.2385016400826
h=0.0001
mx=my=mj=-1
limit=2500
epsilon=1
resolution1=500
resolution2=2000
px1,py1,pz1=getGeodesicPath(x,y,a,b,h,epsilon,limit)
px2,py2,pz2=getGeodesicPath(a,b,x,y,h,epsilon,limit)
pathx=px1+px2[::-1]
pathy=py1+py2[::-1]
pathz=pz1+pz2[::-1]
t=len(pathx)//resolution2
r1,r2=norm(x-200,y-200),norm(a-1400,b-1400)
dx1,dy1,dx2,dy2=(x-200)/r1,(y-200)/r1,(a-1400)/r2,(b-1400)/r2
linex1=[200+i*dx1*r1/resolution1 for i in range(resolution1)]
liney1=[200+i*dy1*r1/resolution1 for i in range(resolution1)]
linez1=[height(200+i*dx1*r1/resolution1,200+i*dy1*r1/resolution1) for i in range(resolution1)]
linex2=[1400+i*dx2*r2/resolution1 for i in range(resolution1)][::-1]
liney2=[1400+i*dy2*r2/resolution1 for i in range(resolution1)][::-1]
linez2=[height(1400+i*dx2*r2/resolution1,1400+i*dy2*r2/resolution1) for i in range(resolution1)][::-1]
fig=plt.figure()
ax=fig.add_subplot(projection='3d')
ax.scatter(linex1+pathx[::t]+linex2,liney1+pathy[::t]+liney2,linez1+pathz[::t]+linez2,marker="o")
plt.show()
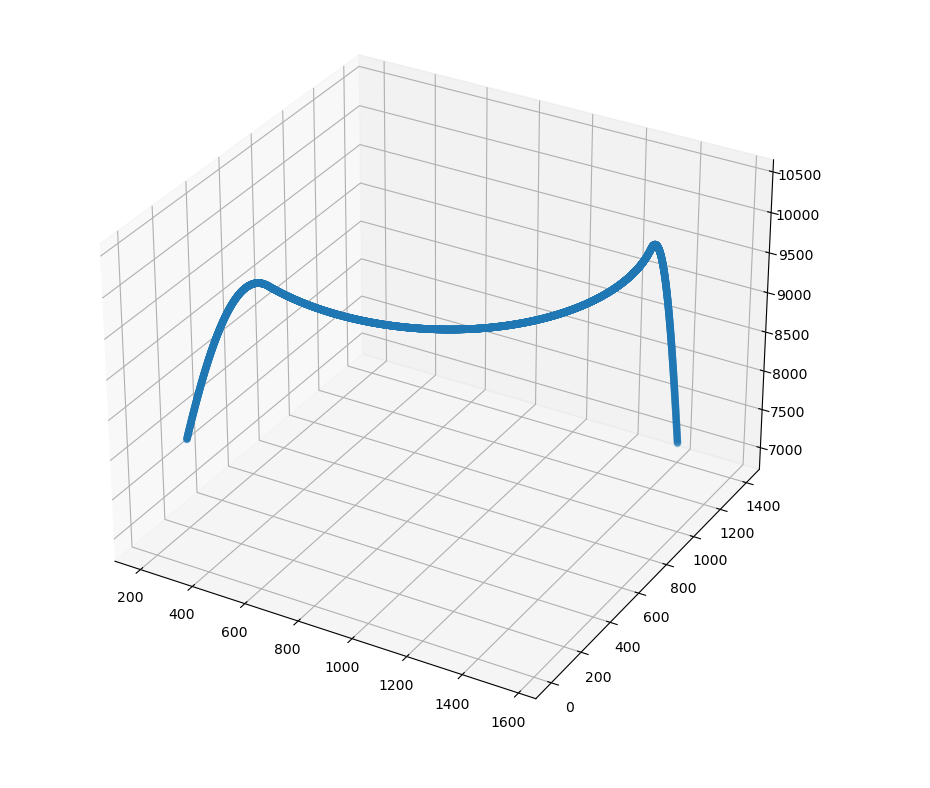
注:本题中的代码均为Python 3,原因一是便于作浮点数计算,二是所使用的库和函数只支持Python 3。
注2:本题涉及的微分内容一般在我国《高等数学》课程中的多元微积分部分讲授。
|