由角平分线定理可得
$$\frac{AE}{EB}=\frac{AC}{CB}=\frac{b}{a}, \quad \frac{AG}{GC}=\frac{AB}{CB}=\frac{c}{a},$$
因此三角形ABC与AEG面积之比k为
$$k=\frac{a+b}{b}\cdot \frac{a+c}{c},$$
即
$$(a+b)(a+c)=kbc.$$
由$0 < a\le\min(b,c)$可得$1 < k\le 4$,且$k=4$仅在$a=b=c$时取到,这样的情况有$33333333$种。
因此接下来只需继续考虑$k=2,3$的情形。令$k'=k-1$,则$k'=1$或$2$,且上式可以写作
$$a^2+(b+c)a-k'bc=0,$$
从而有
$$a=\frac{-(b+c)+\sqrt{b^2+c^2+(4k'+2)bc}}{2}.$$
因此存在自然数d,使得
$$b^2+c^2+qbc=d^2,$$
其中$q=4k'+2$(即$q=6$或$10$)。令$x=b/d$,$y=c/d$,则有
$$x^2+y^2+qxy=1.$$
在该双曲线上取点$(-1,0)$,在y轴上取点$(0,t)$,两者确定直线$L_t: y=tx+t$,该曲线上的有理点即$t\in\mathbb Q$该曲线与$L_t$的另一个交点。(见注1)
将$y=tx+t$带入并整理得
$$(t^2+qt+1)x^2+(2t^2+qt)x+t^2-1=0.$$
解之得
$$x=\frac{-(2t^2+qt)\pm|qt+2|}{2(t^2+qt+1)}.$$
按本题的设定,$x,y$都是正数,因此$t$只能取$0$到$1$之间的值(可以从双曲线的图中看出,两者的尺寸不同,但形状相同)
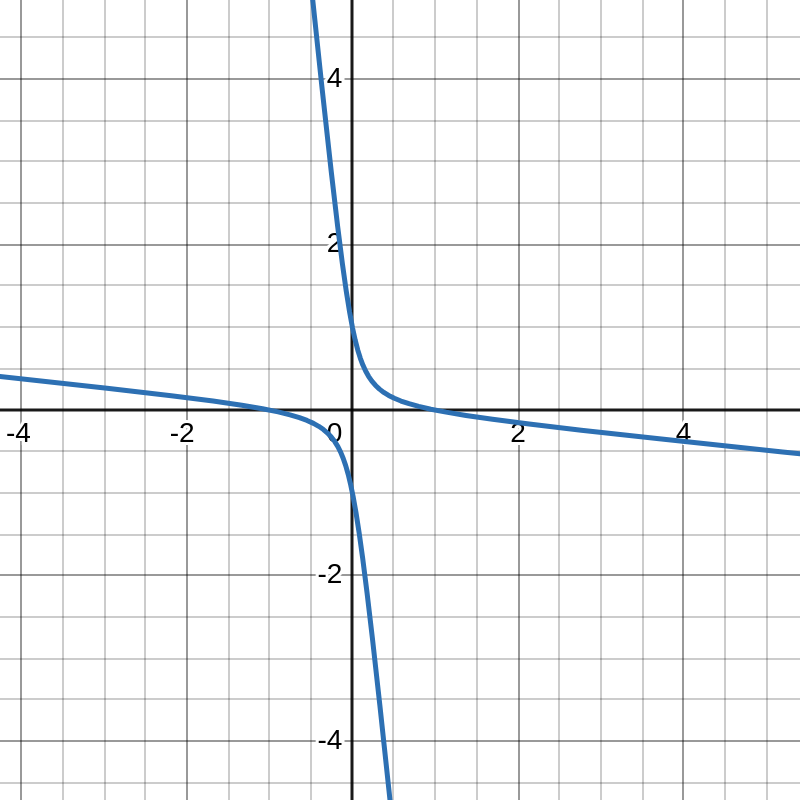
从而有
$$x=\frac{1-t^2}{t^2+qt+1}, \quad y=tx+t=\frac{qt^2+2t}{t^2+qt+1}$$
令$t=m/n$,就得
$$x=\frac{n^2-m^2}{m^2+qmn+n^2}, \quad y=\frac{qm^2+2mn}{m^2+qmn+n^2}$$
从中可得一组有效的公式
$$b=\min(n^2-m^2, qm^2+2mn), \quad c=\max(n^2-m^2, qm^2+2mn), \quad a=\frac{d-b-c}{2}=\frac{(2-q)m^2+(q-2)mn}{2}$$
遍历互素的m,n并生成a,b,c,设$d=\gcd(a,b,c)$,并令$a'=a/d, b'=b/d, c'=c/d, p'=a'+b'+c'$,那么筛选出满足$0 < a'\le b'\le c'$、$a'+b'>c'$的值后根据$(a',b',c')$去重,每一组$(a',b',c')$对应$\lfloor10^8/p'\rfloor$个解。
$d>1$的情况普遍存在,难以直接从上式获得m,n的范围,经尝试可得n需超过20000,但不超过25000,最终结果是$139012411$。
注:可以参考UTM系列教材(Undergraduate Text in Mathematics)中《椭圆曲线上的有理点》(Rational Points on Elliptic Curves, by J.Silverman, J.Tate)第一章。
注2:本题计算量非常大,需要较长的运行时间,代码中打印了进度信息。
from fractions import gcd
bound=10**8
r=33333333
for q in [6,10]:
s=set()
for n in range(2,25000):
for m in range(1,n):
if gcd(m,n)==1:
a=((q-2)*m*n+(2-q)*m*m)/2
b,c=n*n-m*m,q*m*m+2*m*n
if b>c:
b,c=c,b
d=gcd(gcd(a,b),c)
a,b,c=a/d,b/d,c/d
p=a+b+c
k=str(a)+"-"+str(b)+"-"+str(c)
if a<=b and a+b>c and p<=bound and not (a==b==c) and k not in s:
s.add(k)
r+=(bound/p)
if n%500==0:print (n/500)+50*(q-6)/4,"percent completed"
print r
|