Minkowski和

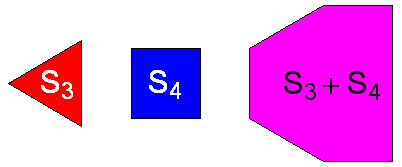
记$S_n$为顶点$v_k=(x_k, y_k)$（$k=1, 2 , \ldots, n$）按如下方式定义的闭（即包括边界和内部）正$n$边形： $$x_k=\cos\left(\frac{2k-1}{n}\times 180^\circ\right) \quad y_k=\sin\left(\frac{2k-1}{n}\times 180^\circ\right).$$ 点集S,T的Minkowski和定义如下： $$S+T=\{(u+x, v+y): (u,v)\in S, (x,y)\in T\}.$$ 例如，$S_3+S_4$是如下图中的粉色六边形： 问$S_{1864}+S_{1865}+\ldots+S_{1909}$是多少边形？

本题难度:

解答

根据凸多边形Minkowski和边界的计算方法，$S+T$的顶点具有$v_i+v_j'$（$v_i\in S, v_j'\in T$）的形式。 而$v_i$和$v_j'$的具体下标是将两组顶点分别按极角排序后用双指针再根据向量$v_iv_{i+1}$和向量$v_j'v_{j+1}'$的极角大小选择后依次生成。若两者不同，则将极角较小者的指针下标进一，否则两指针同时进一。 由此可见，最终结果只和各边的极角所组成的集合大小有关。 若令$\omega=e^{2\pi i/2n}$，并把$S_n$的顶点标记在复平面上，则它们对应$\omega, \omega^3,\ldots, \omega^{2n-1}$，相加得 $$\omega+\omega^3+\ldots+\omega^{2n-1}=\omega(1+\omega+\ldots+\omega^{2n-2})=\omega\cdot\frac{1-\omega^{2n}}{1-\omega^2}=0.$$ 因此$S_n$的中心在原点。 显然选择合适的基准线后作为$x$轴（在本题中事实上是$y$轴）重新建立坐标系后，$S_n$各边界的极角将是$2k\pi/n$，其中$k=0,1,\ldots, n-1$。 根据上述构造，只需找出分母在$1864$到$1909$之间的所有真分数的总数，结果是$86226$。 import fractions print len(set(fractions.Fraction(a,b) for b in range(1864,1910) for a in range(b)))