每个球的直径都大于管内半径,因此球不能并排放置,而只能在管内用斜向相切的方式堆叠,如下图(图来自此帖):
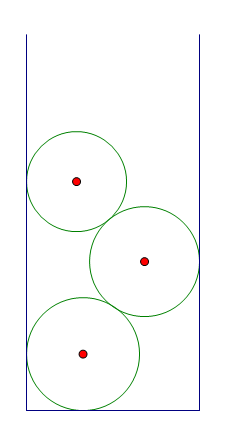
若上下两圆的半径分别为$r_1, r_2$mm,则容易看出两者球心的高度差是
$$d(r_1,r_2)=\sqrt{(r_1+r_2)^2-(100-r_1-r_2)^2}=\sqrt{200(r_1+r_2)-10000}=10\sqrt{2(r_1+r_2)-100}.$$
假设球体已按管长最短的方式排列,想像将该管首尾相接,连成一环状管路,记其周长为C。
若在半径分别为$r_1, r_2$mm的两个球之间将这一环状管路分开,就可得一直管,此时直管的长度为
$$C-d(r_1,r_2)+r_1+r_2=C+r_1+r_2-10\sqrt{2(r_1+r_2)-100}$$
令$x=r_1+r_2$,则管长为$C+x-10\sqrt{2x-100}$,按题设,x在61和99之间,容易看出此时该函数为减函数,因此直管两侧的球半径之和必定是环状管路中相邻两球半径之和的最大值。
现将该直管两侧的球移除,得一由19个球堆成的直管,可以发现该直管两侧的球半径之和仍需是最大值,否则将其连成环管后重新插入移除的两球可得更小的管长,与假设矛盾。
不断重复上述步骤,可得一启发性的结论,该管左右两侧的球半径从外向内依次减小,比较左右两侧分别放置半径为$(x+2, x)$,$(x+1,x+3)$和$(x+3, x)$,$(x+1,x+2)$两种方法可知前者更优。
因此可以猜测该排列左右两侧分别是奇数和偶数,且从外向内依次减小,即
$$49, 47, 45, 43, 41, 39, 37, 35, 33, 31,30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50,$$
将这些数从左到右依次标记为$r_1,\ldots,r_{21}$,则管长为
$$49+50+\sum_{k=1}^{20}10\sqrt{2(r_k+r_{k+1})-100}\approx 1590.933116150962,$$
即$1590933$微米恰是答案。
本题无需编程。
|