龙形曲线
|
记$D_0$为包含两个字符的字符串Fa。$D_n$是通过如下字符串替换规则由$D_{n-1}$递推得到的字符串:
\begin{align*}
a \mapsto& aRbFR \\
b \mapsto& LFaLb \\
\end{align*}
因此$D_0=Fa$,$D_1=FaRbFR$,$D_2=FaRbFRRLFaLbFR$,依此类推。
忽略a,b,把F看作前进一步,L看作左转90度,R看作右转90度,并规定起始位置是是$(0,0)$,面向$(0,1)$,就可以由$D_n$画出一条行进轨迹。
这种轨迹称作龙形曲线。例如下图$D_{10}$所对应的曲线,若把每个F算作一步,那么高亮的点$(18,16)$是在第500步所到达的位置。
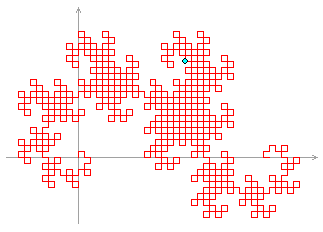
根据$D_{50}$绘制图象,写出第$10^12$步时的坐标$(x,y)$,以“x,y”的形式给出结果(中间没有空格,两侧也没有括号)。
|
本题难度:
|
解答
|
不难看出$D_n$中共有$2^n$步,因此$D_n$所对应的字符串非常长,直接计算是不可行的。
将$D_{n-1}$所对应的曲线以最后一步所在的位置为端点逆时针旋转90度后得到一条新的曲线$D_{n-1}'$。
根据维基百科Dragon Curve页面(大陆地区无法访问)的信息,$D_n$就是$D_{n-1}$与$D_{n-1}'$的拼接(两者可以直接拼接,因为根据构造,$D_{n-1}$的终点就是$D_{n-1}'$的起点)。
因此要计算第m步所在的位置$P_m$,先找到最大的、满足$2^n < m$的$n$,$P_m$就在曲线$D_{n+1}$上。
根据构造,$P_m$就等于$P_{2^{n+1}-m}$绕$P_{2^n}$逆时针旋转$90$度所得的点。
若把从原点到$P_{2^{n+1}-m}$所对应的向量记作$v=(x,y)$,将其逆时针旋转$90$度所对应的向量记作$v'=(-y,x)$,那么$P_m$也可以看作以$P_{2^{n+1}}$为起点,行走$v'$所得。
类似地,若把从原点到$P_{2^n}$所对应的向量记作$u=(x',y')$,将其顺时针旋转$90$度所对应的向量记作$u'=(y',-x')$,则$P_{2^{n+1}}$就是从$P_{2^n}$出发,再移动$u’$所得,因此其坐标是$(x'+y',y'-x')$。
如此递归计算即得结果$139776,963904$。
注:以下为Python 3代码,因记忆化搜索需要的@cache装饰器是Python 3的新特性。
from functools import *
@cache
def pos(n):
if n < 2:
return 0,n
else:
m=1 << len(format(n,"b"))
if n*2==m:m//=2
x,y=pos(m>>1)
dx,dy=pos(m-n)
return x+y-dy,y-x+dx
print("%d,%d" %pos(10**12))
|
| |