成本偏斜编码
|
设A和B均为比特串(由0和1组成的序列)。
若从B的左端取和A的长度相等的比特位所得的子串恰好等于A,就称A为B的前缀。
例如,00110是001101001的前缀,但不是00111或100110的前缀。
n元无前缀编码是指由n个不同的比特串组成的集合,这些比特串间两两都不互为前缀。
例如,$\{0000, 0001, 001, 01, 10, 11\}$就是一种六元无前缀编码。
现假定传输比特位0的花费是一分钱,而传输比特位1的花费是四分钱。
那么,上述六元无前缀编码的总花费是35分钱,恰是总花费最低的六元无前缀编码。
记$Cost(n)$总花费最低的n元无前缀编码的费用,例如$Cost(6)=35$。
求$Cost(10^9)$。
|
本题难度:
|
解答
|
基本策略与霍夫曼编码一致。
考虑这样一种二叉树,根节点的值为空串,表示比特串的起始,其它所有节点的值均为0或1,可以规定若当前节点是其父节点的左子节点,则其值为0,否则值为1。
每一条从根节点到每一个叶节点的路径都唯一对应一个比特串,n元无前缀编码就可以按此方式形成一颗有n个叶节点的二叉树,例如题面中的六元无前缀编码对应二叉树:
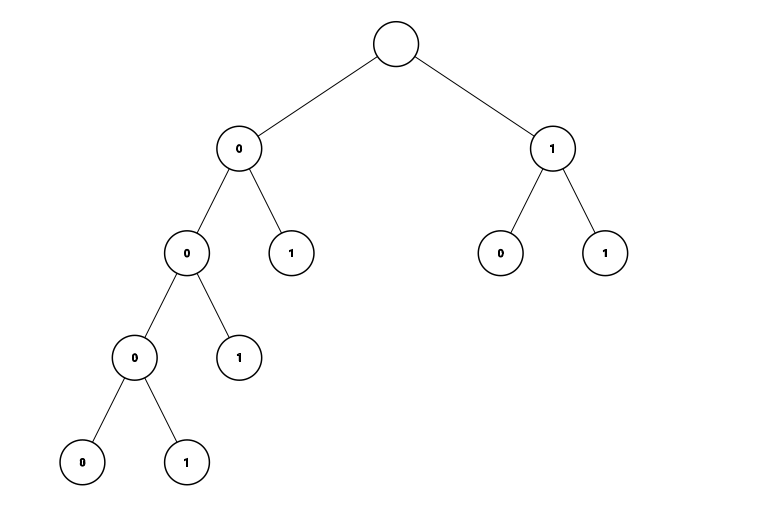
为叙述方便,以下行文中不区分n元无前缀编码及其所对应的二叉树。
用$T_n=\{a_1,\ldots,a_n\}$表示一个n元无前缀编码,并用$|a_k|$表示编码$a_k$的花费。
记$\|T_n\|_{\ell^{\infty}}$为$T_n$中的编码的最大花费,记$\|T_n\|_{\ell^{1}}$为$T_n$中的编码的总花费。
令$c(i)$为最大花费不超过i的情况下的最多的编码数,即
$$c(i)=\max\{n: \|T_n\|_{\ell^{\infty}}\le i\}.$$
记$T_{c(i)}^*$为满足上述要求、且总费用最低的树,注意由此定义可知这样的树是唯一的。
对$c(i)$而言,有初值$c(0)=c(1)=c(2)=c(3)=1$,以及递推式
$$c(i)=c(i-1)+c(i-4).$$
这是因为由最大性可以分别在$T_{c(i-1)}^*$的所有编码前添加一位$0$和$T_{c(i-4)}^*$的所有编码前添加一位$1$,再将两者合并来得到$T_{c(i)}^*$。
再令
$$s(i)=\|T_{c(i)}^*\|_{\ell^1},$$
则有初值$s(0)=s(1)=s(2)=s(3)=0$(注意一元无前缀编码中总费用最低的是空树),再由$c(i)$的递推构造可得
$$s(i)=s(i-1)+s(i-4)+c(i-1)+4c(i-4).$$
设m是满足$c(m)\le 10^9$中最大的数,要计算$Cost(10^9)$,还需在$T_{c(m)}^*$中再添加$10^9-c(m)$条编码。
由$T_{c(m)}^*$叶节点数的最大性可知只能扩展那些费用不小于$m-3$的叶节点。
在这样的叶节点下添加两个子节点,相当于在$\|T_{c(m)}^*\|_{\ell^1}$中先移除$m-k$($k=0,1,2,3$),再添加$m-k+1$和$m-k+4$,因此总费用增加$m+5-k$。
为使扩展后的总费用最低,应按k的值从大到小开始扩展,实现中经计算可以验证费用为$m-3$的节点数超过$10^9-c(m)$个,因此只需扩展这一种类型的节点即可。
最后结果为
$$s(m)+(10^9-c(m))\cdot(m+2)=64564225042.$$
target=10**9
c=[1,1,1,1]
s=[0,0,0,0]
while c[-1]<=target:
s.append(s[-1]+s[-4]+c[-1]+4*c[-4])
c.append(c[-1]+c[-4])
print (target-c[-2])*len(c)+s[-2]
|
| |