钝角三角形
|
令点集
$$S(r)=\{(x,y)\in\mathbb Z^2: |x|+|y|\le r\},$$
记O为原点$(0,0)$,C为点$(r/4,r/4)$。
在$S(r)$中取一点$B$,使得三角形OBC是钝角三角形,记所有这样的点B的数量为$N(r)$。
例如,$N(4)=24$,$N(8)=100$,求$N(10^9)$。
|
本题难度:
|
解答
|
设B的坐标为$(x,y)$,则有
$$|OB|^2=x^2+y^2, \quad |OC|^2=\frac{r^2}{8}, \quad |BC|^2=(x-\frac{r}{4})^2+(y-\frac{r}{4})^2,$$
用余弦定理来计算,若O处为钝角,则有$|OB|^2+|OC|^2 < |BC|^2$,即
$$x^2+y^2+\frac{r^2}{8} < (x-\frac{r}{4})^2+(y-\frac{r}{4})^2 \quad \Rightarrow \quad 0 < -\frac{r}{2}(x+y) \quad \Rightarrow \quad x+y < 0.$$
若C处为钝角,则有$|BC|^2+|OC|^2 < |OB|^2$,即
$$(x-\frac{r}{4})^2+(y-\frac{r}{4})^2+\frac{r^2}{8} < x^2+y^2 \quad \Rightarrow \quad \frac{r^2}{4}-\frac{r}{2}(x+y) < 0 \quad \Rightarrow \quad x+y>\frac{r}{2}.$$
若B处为钝角,则有$|BC|^2+|OB|^2 < |OC|^2$,即
$$(x-\frac{r}{4})^2+(y-\frac{r}{4})^2+x^2+y^2 < \frac{r^2}{8} \quad \Rightarrow \quad 2(x^2+y^2)-\frac{r}{2}(x+y) < 0 \quad \Rightarrow \quad (x-\frac{r}{8})^2+(y-\frac{r}{8})^2 < \frac{r^2}{32}.$$
最后,B不能在直线OC上,即$x\neq y$。
这些区域的分布如下(图片来自此帖):
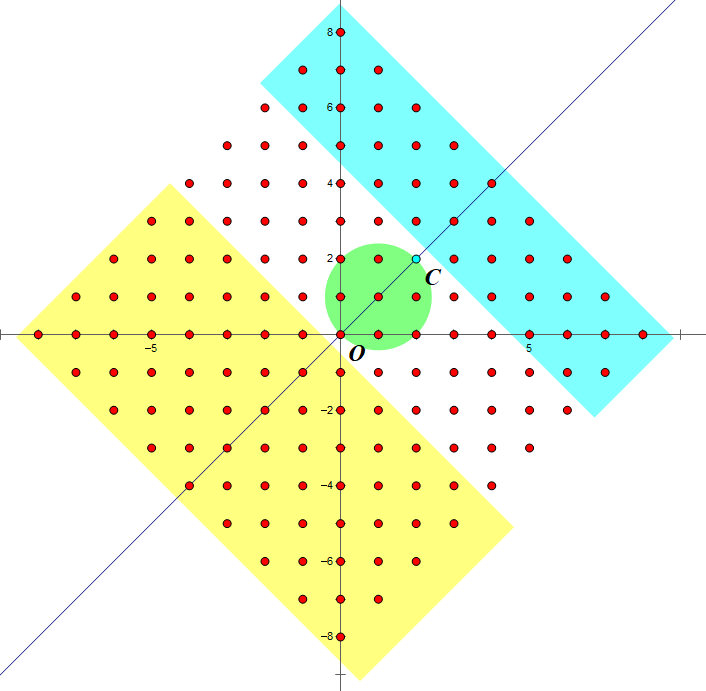
先考察O或C处为钝角的情况,直线$x+y=b$与$S(r)$的交点,是该直线上在$y-x=r$和$y-x=-r$之间的部分,两者各自与$x+y=b$联立,得$(b-r)/2\le y \le (b+r)/2$。
因此当b为偶数时,有$r+1$个整点,再排除$x=y$的情形,共有r个整点,当b为奇数时,共有r个整点,此时若$x=y$, 则有$x=y=b/2$不为整数,因此无需排除。
当O处为钝角时,b可从-1取至-r,因此共有$r^2$个满足要求的点。
当C处为钝角时,b可从$r/2+1$取至r,因此共有$r^2/2$个满足要求的点。
现在考虑B处为钝角的情况,由于$r/8$是整数,平移坐标系,就等同于考察$x^2+y^2 < r^2/32$内整点的数量,这是一个著名的问题,即高斯圆问题(可以参考这里)。
并没有很好的解析公式来描述这一数量,只能遍历计算。
取$n=r^2/32$,先考虑第一象限$x,y>0$内的点,x可以从1取到不超过$\sqrt{n}$,对每个x,y可以从$1$取到不超过$\sqrt{n-x^2}$,因此四个象限内点的数量是$4\sum\limits_{x=1}^{\lfloor\sqrt{n}\rfloor}\lfloor\sqrt{n-x^2}\rfloor$。
根据OEIS A004018中的公式,由于$n=3125\times 10^{13}=5^{18}\times 2^{13}$,圆周上的点共有$4\cdot(18+1)=76$个,需要排除。
再考虑x轴正半轴$x=0, y>0$上的点,此时$y < \sqrt{n}$,x轴负半轴、y轴正半轴、y轴负半轴的情况也相同,因此两坐标轴上(不包括原点)点的数量是$4\lfloor\sqrt{n}\rfloor$。
最后,若$x=y$,则$x^2+y^2 < r^2/32$简化为$|x| < r/8$, 不包括原点共有$r/4-2$个点需要排除。
综上,最终结果为
$$\frac{3r^2}{2}-(\frac{r}{4}-2)-76+4\lfloor\sqrt{n}\rfloor+4\sum_{x=1}^{\lfloor\sqrt{n}\rfloor}\lfloor\sqrt{n-x^2}\rfloor=1598174770174689458.$$
注:本题需要大量细致的初等计算,并且最后的循环有近2亿次,运行时容易假死。
注2:以下代码为Python 3,因math.isqrt是Python 3的新函数。
import math
r=10**9
n=r*r//32
m=math.isqrt(n)
print(r*r*3//2-r//4-74+4*m+4*sum(math.isqrt(n-x*x) for x in range(1,m+1)))
|
| |