本题不太容易想像,并且需要用到一些普通读者不太可能学到的图论定理。
考虑一个正五边形,选定一个正方向,比如逆时针,相邻两点间沿着这一方向可以形成一个向量,总共有五个这样的向量,依次标记为加法群$\mathbb Z_5$中的元素,如下图(图片来自此帖)
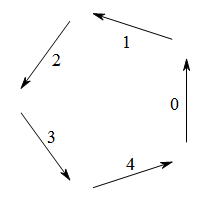
始终把机器人走出的第一步作为方向0,则此后每一步都是这五个方向之一,且根据题中设定(此处不易想像,可自行画图理解),若当前步的方向是i,则下一步只能是方向$i+1$或$i-1$。这里的加减法都在$\mathbb Z_5$中运算。
机器人可以沿着正方向$i\to i+1$遍历,也可以沿着负方向$i\to i-1$遍历,完整遍历一次$\mathbb Z_5$分别对应逆时针和顺时针一周的运动,如下图(图片来自此帖):
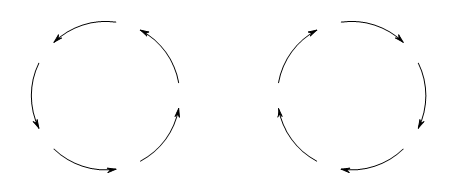
因此若机器人能回到原点,那么它应该完成了$70/5=14$次$\mathbb Z_5$的遍历,也就是在每个方向上所走的步数都各走了14次。
假设机器完成了k次逆时针遍历和$14-k$次顺时针遍历,那么可以把其视作是在由$\mathbb Z_5$的五个节点组成的图上运动,其中从i到$i+1$有k条相同的边,从i到$i-1$有$14-k$条相同的边,需要求出其中欧拉回路(通过图中每条边恰好一次的回路)的总数。
BEST定理给出了这一数量为$\left(13!\right)^5t_r$,其中$t_r$是以图中任意节点为根(对有向欧拉图而言,以任意节点为根所得的结果都一样)所得的内向树形图(也称根向树形图,是指该图实际是一颗数,且所有的边都从子节点指向父节点)的总数。
$t_r$的值由矩阵树定理给出:
$$t_r=\det(L^{(i,i)}),$$
其中$L^{(i,i)}$是$L_{i,i}$的余子式(即从L中划去第i行和第i列后所得的子阵),L是该图的出度Laplace矩阵,它等于各节点出度组成的对角阵D减去该图的邻接阵A($A_{i,j}$等于从i到j的边数量)。
从而在本题中有
\begin{align*}
L&=\begin{pmatrix}14 &&&& \\ & 14 &&& \\ && 14 && \\ &&& 14 & \\ &&&& 14 \end{pmatrix}-\begin{pmatrix} & k & & & 14-k \\ 14-k & & k && \\ & 14-k & & k & \\ && 14-k & & k \\ k &&& 14-k & \end{pmatrix} \\
&=\begin{pmatrix} 14 & 14-k & & & k \\ k & 14 & 14-k && \\ & k & 14 & 14-k & \\ && k & 14 & 14-k \\ 14-k &&& k & 14\end{pmatrix}
\end{align*}
这是一个循环阵(circulant matrix),划去比如第一行第一列后得一Toeplitz三对角阵,不过由于该矩阵非常小,此处不需要利用这些矩阵的结构定理可以直接计算得
$$t_r=\det(L^{(1,1)})=k^4-28k^3+784k^2-8232k+38416,$$
最后,考虑到机器人实际上可以14个0方向中的任意一个出发,并且两节点间的所有边都相同,还需要乘以14,并除以$k!(14-k)!$,综上可得结果
$$\sum_{k=0}^{14}13!\cdot (k^4-28k^3+784k^2-8232k+38416)\cdot\frac{14}{k!(14-k)!}=\sum_{k=0}^{14}\binom{14}{k}(k^4-28k^3+784k^2-8232k+38416) $$
右侧的式子可以手动计算,也可用Wolfram Alpha等计算得$331951449665644800$。
注:本题无需编程,但题中涉及的图论知识一般涵盖在NOI级别的竞赛课程中,题中涉及的线性代数知识是我国本科《线性代数》课程的标准内容。
|