想像有三面镜子按反射面朝内放置的方式摆成正三角形，仅三个顶点处可容一束激光通过。

记三个顶点分别为A,B,C。从C处射入的激光，经过恰好11次反射后再从C处射出，这样的路径一共有两条：其中一条如下所示，另一条是将其反向所得的路径。

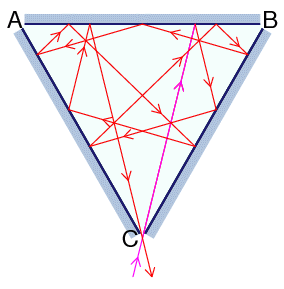
从C处射入的激光，经过恰好1000001次反射后再从C处射出，这样的路径一共有80840条。

从C处射入的激光，经过恰好12017639147次反射后再从C处射出，这样的路径一共有多少条？

本题难度:

将三角形ABC以边为对称轴不断作镜面对称图形，如下图（图来自此贴）：

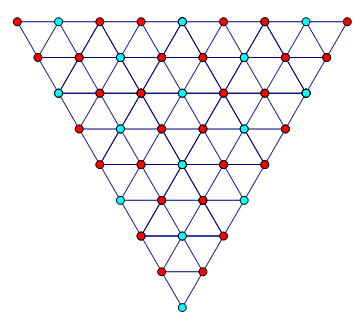
则激光的路径可以视作是上图中的一条直线。

A、B、C的所有对称点（通过有限次镜面对称所得到的点）形成平面上的格（Lattice），这个格可以由向量$\vec a=\overrightarrow{CA}$和$\vec b=\overrightarrow{CB}$生成，将其记作L。

若激光能从C点射出，即存在C的某个对称点，使之在该射线上，且是该射线在C之后的与L的第一个交点。

以C为原点，L中的点都可以用$\vec a$和$\vec b$的整系数线性组合 $x\vec a+y\vec b$表示，以下就用坐标系数对$(x,y)$表示L中的点。不难看出C的所有对称点的坐标满足$x,y>0$且 $$y-x=0 \pmod 3.$$ 也从而原点与该对称点的连线不会与A或B的对称点相交。

进一步观察可以发现，若过原点的直线与L交于C的某个对称点$(x,y)$，那么该直线与$x-1$条平行于$\vec b$的网格线、$y-1$条平行于$\vec a$的网格线和$x+y-1$条平行于$\vec a-\vec b$的网格线相交，即总共反射了 $$x-1+y-1+x+y-1=2(x+y)-3,$$ 次。因此满足题意的C的对称点都在直线 $$x+y=(12017639147+3)/2=6008819575,$$ 上。由于6008819575模3余1，因此有 $$x=y=2 \pmod 3.$$ 此外，应有$\gcd(x,y)=1$，否则若$\gcd(x,y)=d>1$，则直线将先与C的另一个对称点$(x/d, y/d)$相交，从而不满足首次相交的要求。

利用辗转相除的条件可以将该条件进一步写作 $$1=\gcd(x,y)=\gcd(x,6008819575-x)=\gcd(x,6008819575).$$ 因此只需统计不超过6008819575、与之互素且模3余2的自然数的总数。

令$F(n)$为直线$x+y=n$上C的对称点的总数，$f(n)$为其中满足$\gcd(x,n)=1$的数量总数。

显然，若$x+y=n$且$d=\gcd(x,y)$，那么可以用双射$x\mapsto x/d, y\mapsto y/d$将之映射到直线$x+y=n/d$上，因此有 $$F(n)=\sum_{d|n}f(\frac{n}{d})=\sum_{d|n}f(d).$$ 由莫比乌斯反演公式可以将上式改写为 $$f(n)=\sum_{d|n}\mu(d)F(\frac{n}{d}),$$ 其中 $$\mu(d)=\begin{cases}1 & d=1, \\ (-1)^k & d\text{是无平方因子数，有$k$个素因子}, \\ 0 & \text{其它},\end{cases}$$ 是莫比乌斯函数。记$\tilde d\in\{0,\pm 1\}$为d模3的余数，则不难看出 $$F(d)=\frac{1}{3}(d-\tilde d),$$ 从而 $$f(n)=\sum_{d|n}\mu(d)F(\frac{n}{d})=\sum_{d|n}\mu(\frac{n}{d})F(d)=\frac{1}{3}\sum_{d|n}\left(\mu(\frac{n}{d})\cdot d-\mu(\frac{n}{d})\cdot\tilde d \right).$$ 由莫比乌斯函数的基本性质可知 $$\mu(\frac{n}{d})\cdot d=\varphi(n),$$ 其中$\varphi$是欧拉Totient函数。接下来注意到 $$n=6008819575=5^2\cdot 11\cdot 17\cdot 23\cdot 29 \cdot 41\cdot 47,$$ 共有7个素因子且其中每个素因子模3都余-1。根据d中素因子5的分布，有以下三种情况：

$5\nmid d$：此时25能整除$n/d$，因此$n/d$不是无平方因子数，从而$\mu(\frac{n}{d})=0$。

$5|d$，$25\nmid d$：此时$n/d$是无平方因子数，且5也能整除$n/d$，设d有$1+k$个素因子，则$n/d$有$7-k$个素因子，显然$1+k$和$7-k$的奇偶性相同，因此$\mu(\frac{n}{d})\cdot\tilde d=1$。

$25|d$：此时$n/d$是无平方因子数，且5不能整除$n/d$，设$n/d$有k个素因子，则$d/25$有$6-k$个素因子，k和$6-k$的奇偶性仍相同，因此仍有$\mu(\frac{n}{d})\cdot\tilde d=1$。

因此有 $$\sum_{d|n}\mu(\frac{n}{d})\cdot\tilde d=2^7=128,$$ 这是因为共有$7$个素因子，每个素因子都有能整除$n/d$和不能整除$n/d$两种情况。

综上所述，可得 $$f(6008819575)=\frac{1}{3}(\varphi(6008819575)-2^7)=\frac{1}{3}(5\cdot 4\cdot 10\cdot 16\cdot 22\cdot 28 \cdot 40\cdot 46-128)=1209002624.$$ 注：本题无需编程，但所需要的代数数论和几何群论知识只有在学习相关方向的数学系高年级本科生或研究生的课程中才有可能涉及到。