染色方案
|
考虑由A单元:
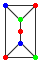
和B单元:
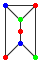
通过将左右两侧各自一条垂直边相互粘贴而组成的图形,如下例:
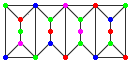
一个$(a,b,c)$型染色方案,是指在一个由a个A单元和b个B单元按上述方式粘贴而组成的图形中用至多c种颜色给每个顶点染色、且相邻顶点颜色不同的构造。
例如只要上例就是一个$(2,2,4)$型染色方案,事实上对于任意$c\ge 4$,上例都是$(2,2,c)$型染色方案。
记$N(a,b,c)$为$(a,b,c)$型染色方案的总数,可以验证
$$N(1,0,3)=24, \quad N(0,2,4)=92928, \quad N(2,2,3)=20736.$$
求$N(25,75,1984)$的最后八位数。
|
本题难度:
|
解答
|
本题涉及到染色多项式的计算,不仅推导困难而且计算也很繁琐。
本题中的A、B两种图并不是常见的几种图或其团和(clique sum),因此染色多项式需要递归计算,图中有7个节点,不论是手动计算还是编程计算都非常麻烦,此处使用Wolfram Alpha辅助计算。
打开Wolfram Alpha页面,输入
Graph{0->1, 0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 0->5, 1->6, 5->6} ChromaticPolynomial
其中0到6分别表示A图中从上到下,从左到右的7个节点,$0->1$表示节点0和1之间存在$1$条边。
根据返回页面给出的结果,A图的染色多项式为
$$P_A(x)=x(x-1)(x-2)(x^4-7x^3+20x^2-29x+19).$$
接下来输入
Graph{0->1, 0->2, 1->2, 2->3, 3->4, 4->5, 4->6, 0->5, 1->6, 5->6} ChromaticPolynomial
可得B图的染色多项式为
$$P_B(x)=x(x-1)(x-2)^3(x^2-2x+3).$$
从而利用染色多项式的团和性质可得一个$(25,75,x)$型染色方案的染色多项式为
$$P(x)=\frac{P_A^{25}(x)P_B^{75}(x)}{x^{99}(x-1)^{99}}=x(x-1)(x-2)^{250}(x^4-7x^3+20x^2-29x+19)^{25}(x^2-2x+3)^{75}.$$
不过A可以在100个可选位置中任意摆放,因此最终的结果为
$$\binom{100}{25}P(1984) \mod 10^8=61190912.$$
写一个快速幂计算多项式的值即可。
b=21015504
z=10**8
x=1984
def qp(a,b):
if b < 5:
return (a**b)%z
else:
c=qp(a,b/2)
return (c*c*a)%z if b%2>0 else (c*c)%z
r=(b*x*(x-1)*qp(x-2,250))%z
u=qp((x*x*x*x-7*x*x*x+20*x*x-29*x+19)%z,25)
v=qp((x*x-2*x+3)%z,75)
print (r*u*v)%z
|
| |